Introduction
The use of crystallization inhibitors has been proposed as a potential preventive treatment method against damage and is extensively tested for crystallization of single salts. However, in practice always mixtures of salts are present. Therefore, before using inhibitors in practice there is a strong need to explore their effect on salt mixtures. In this research, we studied the effect of ferrocyanide ions on NaCl crystallization in salt mixtures of NaCl - LiCl. In this study, a specially designed Nuclear Magnetic Resonance (NMR) set-up was used (see fig 1). NMR is used for carrying out non-destructive, quantitative and simultaneous measurements of hydrogen (H), sodium (Na) and lithium (Li) ions in the droplet To obtain visual information time lapse microscopy of the crystallization was performed using a Dino-lite© digital microscope. Four LED’s were placed at the bottom of the sample holder to provide additional lighting within the enclosed NMR set-up. The capture of photomicrographs along with the NMR measurements gives the possibility to visualize the drying droplet while simultaneously obtaining information about the amount of dissolved salt ions. 




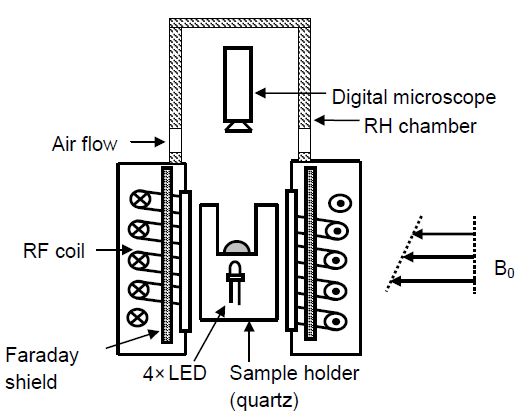Fig 1 Schematic diagram of NMR set-up used for droplet drying experiments. A 300 μl droplet was placed on a quartz glass holder.
 Time lapse microscopy of the drying droplet was performed by incorporating a digital microscope in the set-up. Using a Perspex chamber
the humidity around the droplet was controlled.



    Paradoxical drying
The ternary phase diagram of a NaCl-LiCl-H2O mixture at 25 oC is given in Fig. 6.7, where the LiCl concentration (m) is plotted as a function of the NaCl concentration [85]. The solubility equilibrium line is shown by a red line. Everywhere on this line NaCl will crystallize and LiCl will precipitate only at very high concentrations, i.e., 19.84 m LiCl and 0.03m NaCl. As an example, the expected paths during evaporation of a solution are shown by the solid lines A, B and C for three different initial ion concentrations


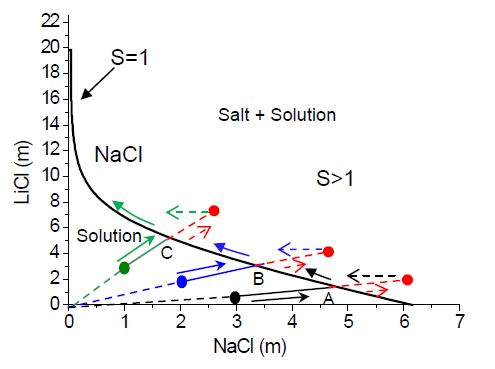
    Fig 2.The ternary phase diagram of NaCl-LiCl-H2O at 25oC. During evaporation the paths A, B and C (shown by solid black, blue and green lines) will be followed for salt mixture of compositions 3m NaCl - 1m LiCl, 2m NaCl - 2m LiCl, and 1m NaCl - 3m LiCl, respectively. If no crystal appears at the intersection of path A, B, C and the equilibrium line (S = 1), the concentration will keep on increasing (supersaturation), as indicated by dotted red arrows. After crystallization the system will return to the equilibrium solubility line.

Three different salt ion concentrations were tested, i.e., 3m NaCl - 1m KCl, 2m NaCl - 2m LiCl, and 1m NaCl - 3m KCl. For all these  experiments, 0.01m inhibitor concentration was used. The results are shown in Fig. 3. The solid lines are the expected paths to be followed upon drying of the droplet. As can be seen from the figure, the experimental data points coincide very well with the expected paths. The salt ion concentration first increases to the equilibrium line. At this point a salt crystal appears, as was confirmed from the pictures taken by the digital microscope. After the onset of crystallization the concentration of NaCl will decrease and the equilibrium solubility line is followed, as shown by dotted arrows. These results show that multi-nuclear NMR is a powerful experimental tool to validate the phase diagrams. For the mixture of NaCl - LiCl also no significantly higher NaCl supersaturation was observed in the presence of inhibitor. These results indicate that in the presence of another salt, ferrocyanide ions are not able to highly supersaturate NaCl.


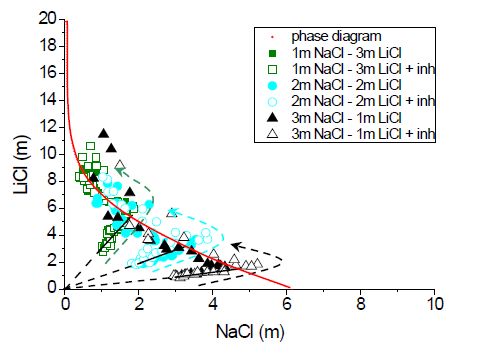Fig 3: The three tested concentrations of NaCl - LiCl salt mixtures shown in the ternary
phase diagram of the NaCl - LiCl - H2O system. The open symbols denote salt mixtures with
inhibitor and the closed symbols denote salt mixtures without inhibitor. The solid lines show
the expected pathways to be followed before the equilibrium line is reached.

However, a clear habit modification was also seen in this case. The pictures showing the crystal morphology at the end of the experiments are shown in Fig. 4, showing the crystal morphology in case of the mixture of NaCl - LiCl without and with inhibitor, respectively. As can be seen in more spreading occurred and dendritic crystals were formed in the presence of inhibitor.

   


Fig 4: Images showing the crystal morphology at the end of the drying experiment for
(a) LiCl and (b) LiCl + 0.01m inhibitor.

    Effect of inhibitor
In the absence of inhibitor after approx. 15 hours, the saturation concentration was achieved in the top few mm of the sample . This causes a dramatic drop in the drying rate for salt saturated brick. Since, most of the salt crystallized as sub-florescence, it causes a more severe blockage of the pores near the drying surface. However, in the presence of inhibitor the crystal morphology changes from cubic to dendritic.  The salt solution  creeps along the branches of the dendrites and transports more and more dissolved salt ions  towards the drying surface causing the efflorescence observed at the end of drying experiment. Pictures of the materials with efflorescence are shown in fig. 4. Approx. 26% and 69% of the salt crystallized as efflorescence in the presence of 0.001 m and 0.01 m inhibitor respectively.  Because of the formation of efflorescence in the presence of inhibitor the average salt ion concentration inside the brick remained below saturation. Therefore, the system remained open and less blockage occurred compared to the salt saturated system without inhibitor. As a consequence of this no dramatic drop in drying rate was seen and the paradoxical disappears.


        Conclusion
 For salt mixtures it is found that the inhibitor will result in a much lower supersaturation than that of the single salt. For both single salt and salt mixtures, the crystal morphology changes completely from bigger cubic crystals to dendritic crystals in the presence of inhibitor. The crystal size decreases significantly at high inhibitor concentrations.

Sonia Gupta, Micheal Steiger, Leo Pel, Klaas Kopinga, The effect of ferrocyanide ions on sodium chloride crystallization in salt mixtures, submitted Crystal Growth and Design (2014)

S.Gupta, Sodium chloride crystallization in drying porous media: influence of inhibitor, Ph.D. thesis, Eindhoven University of Technology (2013)
(Download 2.6 Mb)