Introduction
One of the main degradation mechanisms of porous building materials is salts crystallization. Dissolved ions can be advected along with moisture penetration into a porous material. The salt ions can accumulate and crystallizes in the pores and can as a result produce cracks due to the build-up of the crystallization pressure. To get a better insight into the salt transport mechanism we looked at a special case, i.e., when a porous material is in contact with salt solution on one side and at the same time is exposed to drying conditions at the opposite side. This situation is often encountered in civil engineering constructions in marine environment, where typically a part of the construction in the (sea)water, as is also often seen in the historic city of Venice. As a result there will be a continuous flux of ions through the material towards the drying surface where it can give crystallization damage, both visual and mechanical. This continuous transport of a salt solution, combined with drying, is often referred to as wick action (see also Fig 1). Whereas this wicking can be identified quite simple in a marine environment, one should also think of monuments in contact with natural groundwater. Ground water contains dissolved salts coming from natural sources such as dissolution of salt in soil, rock, and organic material, or human activities such as agricultural chemicals etc. Although the salt concentration might be very low, salts can still accumulate over many years or decades at the drying surface and give rise to damage.



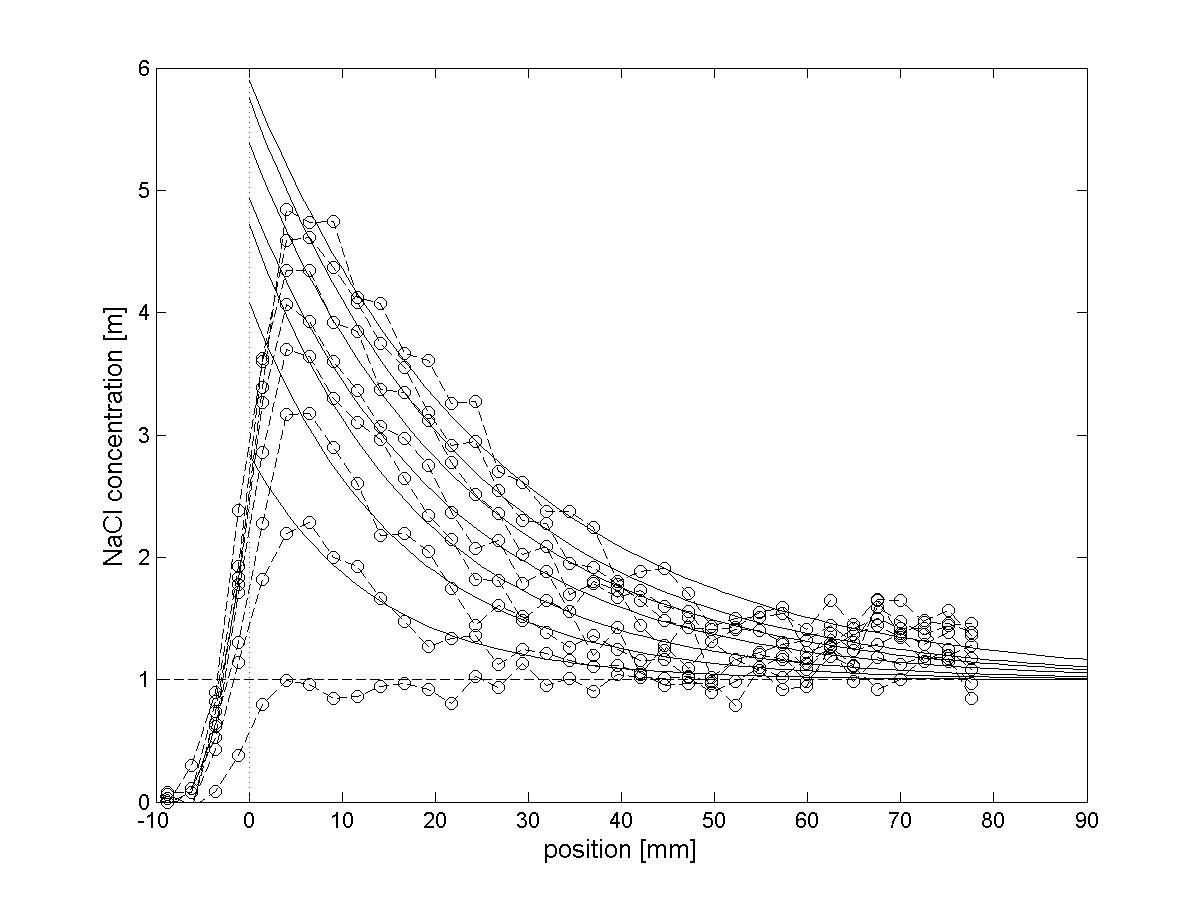
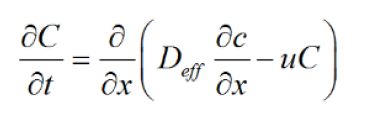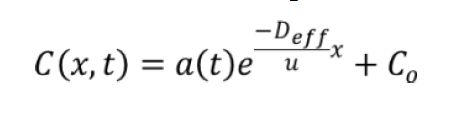Fig 1 A schematic representation of combined wicking and drying of a masonry wall. The bottom of the wall is absorbing a salt solution, e.g., seawater, whereas at the same time the top of the wall  side is drying. As a result there will be a continuous flow of ion towards the drying surface resulting in damage

    Theory
During wick action salt ions will move by two transport mechanisms, i.e., advection and diffusion. Advection is the process of ions moving along with the moisture flow. Hence this process will be determined by the drying conditions at the surface. Diffusion is dependent on the concentration gradient, i.e., diffusion tries to level off any concentration gradient. As a result the net ion flux through the material will be a competition of these two processes. As long as the sample stays saturated during the combined wicking and drying action, as we will assume in this study, the ion salt transport can be described by a combined advection-diffusion equation as given by

 where C is the ion concentration, Deff the effective macroscopic diffusivity of the ions within the porous material and u the macroscopic velocity of the liquid in the porous material, i.e., the Darcy speed. The macroscopic diffusivity of the ions within a porous material is related to the microscopic diffusivity of the ions through the pores by the tortuosity. This equation will be valid as long as there is no crystallization taking place else a sink term has to be added to the right-hand side of this equation.
In the case of drying as studied here, the boundary condition for ions at the drying surface is given by a no flux boundary, i.e., q=0, and hence i.e.; 

Whereas the flux boundary condition at the wicking surface, where the salt solution is absorbed is given by:

where Co is the concentration of the salt solution being absorbed at the wicking surface. As we have in our experiment a constant boundary condition, we can assume that in first order the liquid flow is constant, i.e., u= constant. As also the concentration of the absorbed salt solution is constant, i.e., C= Co, we can in this case solve the differential equation giving the concentration c(x,t) as a function of time and position, i.e.;


Where a(t) is a constant which is a function time. Hence this solution tells us that the concentration in the sample can be described by a simple exponential decay. In addition it indicates that characteristic width of the salt concentration peak, given by 4Deff/u and hence is  determined by the ratio of the liquid velocity and diffusivity.



    Results
The results of the combined wicking and evaporation experiment are given in fig 2. Although the NaCl concentration profiles were measured every 3 hours, here we have given the profiles every 5 days for the first 40 days of the experiment, reflecting the slow process. As can be seen from these NaCl profiles the concentration near the surface slowly increases, whereas the concentration of the back remains constant at 1 m (mole/kg), reflecting the constant concentration of the inflow and of the reservoir. On the other hand we do not see the concentration rising to the saturation concentration of 6.1m as to expected for NaCl. Indeed if we inspect the profiles closer, the NaCl concentration rises from almost 0 at the position 4 mm outside of the sample, i.e., in the air, to maximum 4 m at the position 4 mm inside the sample. This gradual increase near the surface is due to 1D-resolution of the NMR, which is averaging each measurement point over 6 mm as explained previously. Hence the 1D resolution is smoothening the real concentration profile within the sample, and the maximum concentration reached within the sample, i.e., the top, will be higher. In order to correct for this problem, we have fitted the model as derived (see Eq. 5) to each individual profile. The results are also given in figure 2. As can be seen each profile can be approximated well by an exponential decay function. We can also see that the interpolation with x=0 indicates that the maximum salt concentration of 6 m is reached after 40 days, which could also been seen from crystals forming at the top of the sample.


Fig 2: The measured Na-concentration profiles as determined by NMR during wick action of a sample of 100 mm in length.
 Dry air is blown over the top ot the sample at x=0, whereas a reservoir of 1m NaCl  is supplied at x=100 mm.
The profiles are given for every 5 days for a total time of 40 days.


     

L. Pel , R. Pishkari , M. Casti, A simplified model for the combined wicking and evaporation of a NaCl solution in limestone, Materials and Structures  51-66 (2018) https://doi.org/10.1617/s11527-018-1187-y  (This paper got Outstanding paper 2018 Award of Materials and structures)
 

Leo Pel, Raheleh Pishkari,Wick action in cultural heritage, SWBSS 2017, 4th International Conference on Salt Weathering of Buildings and Stone Sculptures, 20-22 September 2017