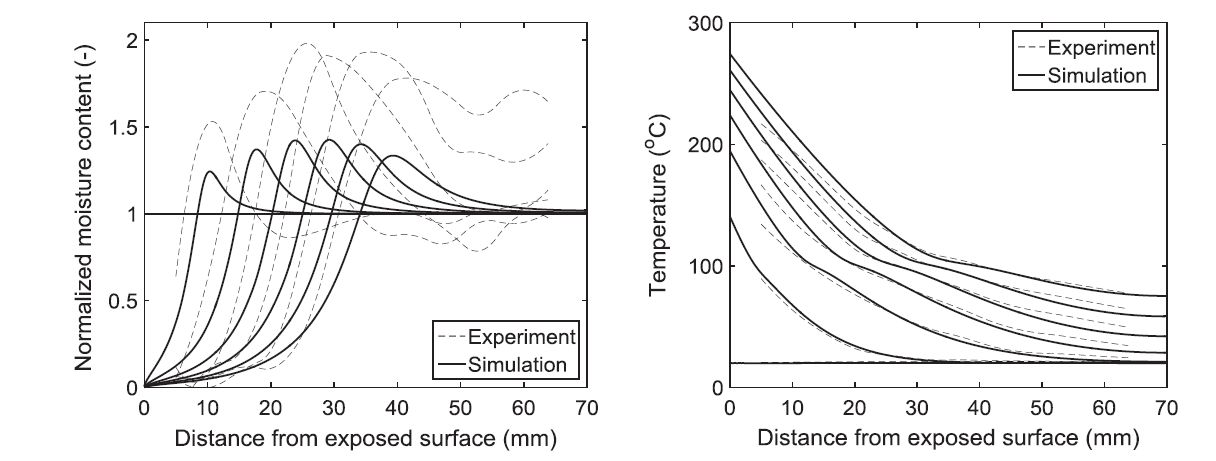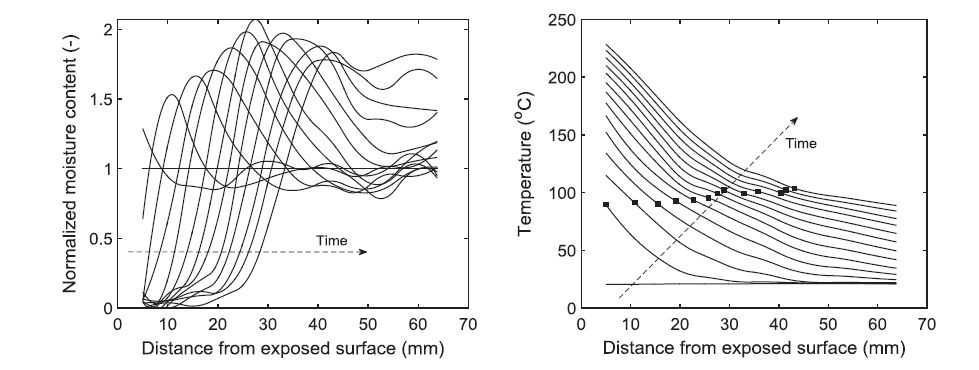
Fig 1 a) Normalized moisture content profiles and (b) temperature profiles during one-sided heating of a pine cylinder,
with its axis in the combined radial/tangential direction. The time between consecutive profiles is 10 minutes.
The position of the peak in moisture content is indicated in each temperature profile with marker.